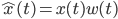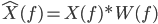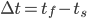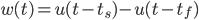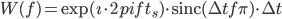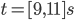Before this, I would recommend reading the Macro Basics Tutorial. In the article we discussed rule 4 that disallowed recursion explicitly. However, this doesn't mean we cant do recursion. The rule states that if we come across the current macros name it is flagged as a macro that cannot be evaluated. The trick here is that we need an indirect macro that refers to macro we want to recurse. If the indirect macro doesn't evaluate during the macros expansion, we can then evaluate it to recurse. This is hard to follow so lets start start building it up with example. The correct code is at the end (so feel free to skip the derivation) but I want to show where everything comes from.
So first step, lets create an indirection to the recursion macro and see what happens:
#define RECURSE(x) x RECURSE_INDIRECT EMPTY () () (x) // This the same as #define RECURSE(x) x DEFER(RECURSE_INDIRECT) () (x) // I just kept the EMPTY() in to make it a bit more explicit #define RECURSE_INDIRECT() RECURSE RECURSE(x) // This evaluates to x RECURSE(x) /* This example is similar to the mutual recursion example When the RECURSE macro is expanded, RECURSE_INDIRECT () is also This causes RECURSE to be added as a result of the initial RECURSE and as a result we disallow it from expanding more */
So the problem is we need to delay the evaluation of the indirection macro so that it is expanded only AFTER the initial macro. How do we do this? We make use of the delay macro discussed before. By adding an EMPTY() we can delay the execution by one step. Lets look at the updated macro
#define EXPR(...) __VA_ARGS__ #define RECURSE(x) x RECURSE_INDIRECT EMPTY () () (x) #define RECURSE_INDIRECT() RECURSE RECURSE(x) // This expands to x RECURSE_INDIRECT () (x)! /* When we call RECURSE(x) after parameter replacement [x RECURSE_INDIRECT EMPTY () (x)] is evaluated to [x RECURSE_INDIRECT(x)]. By adding the EMPTY() we were able to defer the execution of RECURSION_INDIRECT. */ EXPR(RECURSE(x)) // This expands to x x RECURSE_INDIRECT () (x) /* We did it! This is the same as expanding EXPR(x RECURSE_INDIRECT () (x)) Since we expand RECURSION_INDIRECT macro (because it is a paramter to the EXPR macro), the RECURSE that is added as a result of the expansion can actually be expanded. This is because RECURSE was a result of the RECURSION_INDIRECT not the RECURSE macro! As a result when we evaluate the result of the expansion RECURSE is evaluated and we have no recursed!. */ EXPR(EXPR(RECURSE(x))) // This expands to x x x RECURSE_INDIRECT () (x)
Note, we must make sure the indirection macro doesn't actually call the macro its indirecting explicitly. At which point the indirection would be added as a result of the expansion of the indirection!
#define RECURSE(x) x RECURSE_INDIRECT EMPTY () (x) #define RECURSE_INDIRECT(x) RECURSE(x) RECURSE(x) // x RECURSE_INDIRECT (x) EXPR(RECURSE(x)) // x x RECURSE_INDIRECT (x) /* Rewrite it as EXPR(x RECURSE_INDIRECT (x)) and we can see we RECURSE_INDIRECT as a result of expanding RECURSE_INDIRECT */ EXPR(EXPR(RECURSE(x))) // As expected we get x x RECURSE_INDIRECT (x)